Quadratic equations are elementary components of algebra, playing a playing a very important role in different fields such as engineering, physics, economics, and even everyday problem-solving. This description is written to provide my viewers a detailed note on the intricacies of quadratic equations, exploring their structure, methods of solution, and real-world applications. Whether you’re a student aiming to master algebra or someone utilizing it for a quick answer to solve a real-world application.

What is a Quadratic Equation?

A quadratic equation is a second-degree polynomial equation in a single variable x, with the general form:

ax²+bx+c=0

Here, a, b, and c are coefficients also known as constants, with a≠0. The term ax² essentially elaborates the quadratic component, bx the linear component, and c the constant term. The presence of the x² term distinguishes quadratic equations from linear equations or other higher degree polynomials, making them a subject of particular interest in algebra.

Historical Background of Quadratic Equations

Quadratic equations have a rich history since back to ancient civilizations. The Babylonians, around 2000 BCE, were known to be the first to solve quadratic equations, albeit using geometric methods. Over the passing years, mathematicians from various cultures, including the Greeks, Indians, and Persians, contributed to developing systematic methods for solving these equations. The quadratic formula, a pivotal tool for finding solutions, was refined during the Renaissance period (a period of immense transformations within Europe), cementing quadratic equations’ place in modern mathematics.

Standard Form of a Quadratic Equation

Quadratic Equation standard form is a fundamental for identifying the coefficients and understanding the equation’s behavior. It is expressed as:

ax2+bx+c=0

• Quadratic Term (ax²): Represents the degree of the equation. The coefficient a determines the parabola’s opening direction (upwards if a>0, downwards if a<0).

• Linear Term (bx): Influences the slope and position of the parabola.
• Constant Term (c): Shifts the parabola vertically on the graph.

The basic understanding of this standard form is essential for applying various methods to solve quadratic equations effectively as polynomials of higher degree do not comply with these methods.

Methods to Solve Quadratic Equations

Different methods of mathematics can be used to solve Quadratic equations; each method has its own advantages depending on the equation’s structure and the desired solution form as per requirement of the user.

1. Factoring

Factoring technique is used to express the quadratic equation as a product of two binomials. This method is efficient when the equation can be easily factored into integers.

Steps to Factor a Quadratic Equation:

1. Express the Equation in Standard Form: Ensure the equation is in the form ax²+bx+c=0.
2. Find Two Numbers: Identify two numbers that multiply to ac and add up to b.
3. Rewrite and Factor: Rewrite the middle term using the two numbers and factor by grouping.

Example:

Solve x²+5x+6=0 by factoring.

1. Find Two Numbers: 2 and 3 multiply to 6 and add to 5.
2. Rewrite: x²+2x+3x+6=0
3. Factor by Grouping: x(x+2)+3(x+2)= 0
4. Solutions: x=−3 or x=−2

Factoring provides quick solutions when applicable but may not always be feasible, especially with non-integer roots.

2. Quadratic Formula

The quadratic formula is a method for solving any quadratic equation, regardless of whether it can be factored easily or not and is applicable on all type of quadratic equations.

Quadratic Formula:

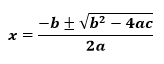
Steps to Use the Quadratic Formula:

1. Identify Coefficients: Determine the values of a, b, and c from the standard form.
2. Calculate the Discriminant (Δ\DeltaΔ): Δ=b2−4ac
3. Determine the Nature of Roots:
   • If Δ>0: Two distinct real roots.
   • If Δ=0: One repeated real root.
   • If Δ<0: Two complex roots.
4. Compute the Roots: Substitute the values into the quadratic formula to find xxx.

Example:

Solve 2x²−4x−6=0 using the quadratic formula.

1. Coefficients: a=2, b=−4, c=−6
2. Discriminant: Δ=(−4)²−4(2)(−6)=16+48=64
3. Nature of Roots: Δ>0, so two distinct real roots.
4. Compute Roots:

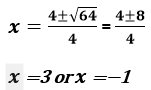
The quadratic formula is reliable and straightforward, making it a preferred method for many mathematicians and students.

3. Completing the Square

Completing the square transforms the quadratic equation into a perfect square trinomial, allowing for easy extraction of the variable’s value.

Steps to Complete the Square:

1. Express the Equation in Standard Form: ax²+bx+c=0
2. Divide by a (if a≠1): x₂+(b/a)x=−(c/a) ​
3. Add (b/2a)² to Both Sides: This creates a perfect square trinomial on the left.
4. Factor the Trinomial: (x+b2a)2=new constant\left(x + \frac{b}{2a}\right)^2 = \text{new constant}(x+b/2a​)²=new constant
5. Take the Square Root of Both Sides: Solve for x.
6. Simplify to Find the Roots.

Example:

Solve x²+6x+5=0 by completing the square.

1. Standard Form: x²+6x=−5
2. Add (6/2)²=9 to Both Sides: x²+6x+9= -5+9=4
3. Factor the Trinomial: (x+3)²=4
4. Take Square Root: x+3=±2
5. Solve for x: x=−3±2 ⇒ x=−1 or x=−5

Completing the square is particularly useful for deriving the quadratic formula and understanding the geometric representation of quadratic functions.

4. Graphing Quadratic Equations

Graphing provides a visual representation of the quadratic equation, allowing for the identification of roots, vertex, and the parabola’s direction.

Steps to Graph a Quadratic Equation:

1. Express in Standard Form: y=ax²+bx+c
2. Determine the Vertex: The vertex (h,k) can be found using:

h=−b/2a

k=f(h)

3. Find the Axis of Symmetry: A vertical line passing through the vertex, x=h.
4. Identify the Direction of the Parabola: Upwards if a>0, downwards if a<0.
5. Plot the Y-intercept: Point (0,c).
6. Calculate Additional Points: Choose values of x around the vertex and compute corresponding y values.
7. Draw the Parabola: Connect the plotted points to form the U-shaped curve.

Example:

Graph y=x²−4x+3.

1. Vertex:

h=4/2(1)​=2

k=(2)²−4(2)+3=4−8+3=−1

Vertex at (2,−1)

2. Axis of Symmetry: x=2
3. Direction: Upwards (a=1>0)
4. Y-intercept: (0,3)
5. Additional Points:
   • x=1: y=1−4+3=0
   • x=3: y=9−12+3=0
6. Plot and Draw: Plot the vertex, y-intercept, and additional points, then sketch the parabola.

Graphing not only aids in solving quadratic equations but also enhances the understanding of their properties and behaviors.

Applications of Quadratic Equations

Quadratic equations extend beyond the confines of algebra classrooms, finding applications in diverse real-world scenarios.

1. Physics

In physics, quadratic equations model projectile motion, where an object’s trajectory forms a parabola starting from the initiating point to the final destination. Calculating the maximum height or the time of flight involves solving quadratic equations. A player hits a six, a soccer player kicks the ball the flight time calculation of the ball is calculated using quadratic equation.

2. Engineering

Engineers are the one who use quadratic equations more than anything in different scenarios of daily business starting from the designing structures, analyzing forces, and optimizing materials. In the field of electronics, mechatronics, aerospace and many more.

3. Economics

Quadratic equations help in optimizing profit and cost functions, where companies aim to maximize profits or minimize costs by analyzing quadratic relationships between variables.

4. Computer Graphics

In computer graphics, quadratic equations assist in rendering curves and surfaces, essential for creating realistic animations and models.

5. Medicine

Quadratic models have a vital utilization in the field of medicine for the analysis of the data gathered from different experiments. This includes the models to predict the growth of bacterial populations or the spread of diseases, aiding in medical research and public health planning. Not only this one example elaborates the utilization of these equations in medical sciences but it has more effective employments for different researches.