Algebraic Fraction Calculator

Fractions are a basic element in the realm of mathematics. We’ve all encountered these in grade school—sharing a pizza among friends, allocating time, or grasping the concept of fractions. However, as we advance to higher levels of mathematics, fractions develop into a more advanced concept: algebraic fractions. These fractions have algebraic expressions, typically involving variables, in the numerator, the denominator, or both. They may appear somewhat daunting at first, but algebraic fractions are a fundamental component of mathematical language and have genuine applications in both academic and practical contexts.

Understanding Algebraic Fractions

Let’s start with the basics. An algebraic fraction is a fraction where the numerator and/or the denominator contains a variable. For example:

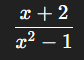
In this case, the numerator and denominator are both algebraic expressions. Just like regular fractions, algebraic fractions can be added, subtracted, multiplied, or divided—but the presence of variables adds a layer of complexity. They need to be simplified with care through factoring expressions, pinpointing common denominators, and comprehending the constraints (such as values that result in a zero denominator).

Students learn important skills by mastering the manipulation of algebraic fractions, including factoring, recognizing variable restrictions, simplifying expressions, and solving intricate rational equations. They are more than mere academic exercises; they serve as the basis for grasping advanced mathematics and addressing real-world issues.

Applications in Engineering and Science

Algebraic fractions find one of their clearest practical uses in the fields of physics and engineering. No matter if they are dealing with voltage in electrical circuits, stress in a bridge beam, or fluid dynamics in a pipe, engineers frequently use equations with variables to model systems. These relationships often include ratios of polynomials or other algebraic expressions.

As an example, take a look at Ohm’s Law from the field of electrical engineering. In the analysis of complex AC (alternating current) circuits, impedance (the equivalent of resistance in AC contexts) is frequently represented with algebraic fractions to illustrate the temporal behavior of current and voltage:

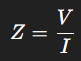
algebraic fractions that engineers work with to create systems that are efficient, safe, and functional.

Likewise, in physics, algebraic fractions emerge when addressing issues connected to speed, acceleration, resistance, and momentum. Expressions often take on a rational form, for example, when calculating material resistance based on temperature and current. These fractions are used by physicists to forecast results, validate theories, or plan experiments.

In the World of Finance and Economics

Though finance might seem far removed from algebraic expressions, it actually relies heavily on mathematical modeling. Economists and financial analysts use algebraic fractions to express relationships between variables like interest rates, investment returns, inflation, and time.

Take, for instance, the compound interest formula:

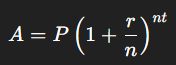
Here, the expression r/n​ is a rational expression, where r is the annual interest rate and n is the number of times the interest is compounded per year. When analysts need to model more dynamic or variable situations—such as shifting interest rates or changing investment terms—algebraic fractions provide the flexibility to adapt the model accordingly.

In supply and demand models, cost and revenue analysis, or break-even calculations, algebraic fractions help represent ratios that change depending on multiple variables. These calculations are essential for business decisions, forecasting, and strategy planning.

In Computer Science and Software Development

In the realm of computer science, algebraic fractions play a crucial role in algorithm design, data processing, and machine learning. When optimizing an algorithm, for example, developers often use mathematical formulas to evaluate efficiency (like time complexity), which can be expressed using algebraic fractions.

Let’s say a function’s efficiency is determined by:

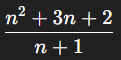
Such an expression can be simplified to understand the program’s behavior as data size grows. This is critical in areas like big data, where systems handle millions or billions of entries, and every fraction of a second matters.

Moreover, in fields like artificial intelligence, predictive models are built using functions that can involve algebraic fractions. These models determine outcomes based on input variables and require simplification and interpretation of expressions, often involving rational functions or expressions derived from data patterns.

Education and Skill Development

Algebraic fractions are also a significant part of mathematics education. They are taught from high school through to college because they develop analytical thinking and problem-solving skills.

Solving problems with algebraic fractions forces students to understand how variables interact, how to simplify expressions, and how to apply multiple steps to reach a logical conclusion. These skills go beyond just math—they’re applicable in law, medicine, management, and any field that requires structured thinking.

The ability to break down a complex problem into manageable parts, isolate variables, and methodically reach a solution is a skill set that has universal value. Whether you’re managing a project, writing code, or diagnosing a medical issue, the logic and precision developed from studying algebraic fractions apply.

Algebraic Fractions in Data Science and Modeling

In the age of data science, professionals use mathematical models to make sense of vast amounts of information. When modeling relationships between variables, rational functions (expressed as algebraic fractions) often provide the best fit.

For example, in regression analysis, sometimes the best way to model a non-linear relationship is through rational regression—a type of modeling that uses algebraic fractions to fit a curve to a dataset. This is particularly useful in fields like epidemiology (studying the spread of diseases), marketing (analyzing consumer behavior), and environmental science (monitoring climate change trends).

Rational expressions are also used in simulation models, where one variable depends on several others in a fractional relationship. These models allow researchers to test different scenarios without real-world risk.

Conclusion

Algebraic fractions are much more than abstract math concepts—they are tools we use every day, whether we realize it or not. From engineering bridges and building efficient algorithms to predicting stock markets and modeling disease outbreaks, algebraic fractions form the backbone of modern problem-solving. As our world becomes more data-driven and technologically advanced, understanding how to work with algebraic expressions, especially in the form of fractions, becomes increasingly valuable. They allow us to represent relationships, understand patterns, and make informed decisions based on logic and evidence. So the next time you come across an algebraic fraction, don’t see it as just another math problem. See it as a universal tool—quietly powering the complex systems that make our modern world function.